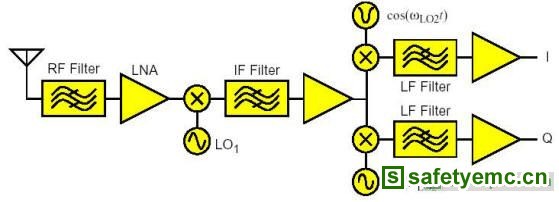
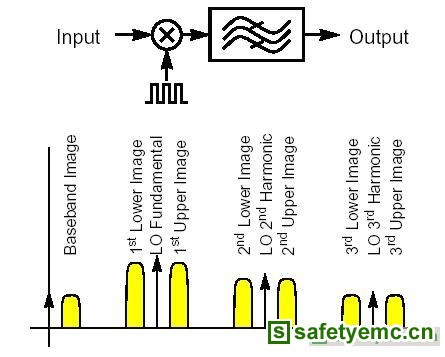
微带线
图五所示的是实际的微带线，其宽度与高度的比率
并不一定要远大于一，且可为
区间中的任意数。典型的高度h是大约数个mm。
边缘效应是无法完全被忽略的，而且关于平行平板线的电场之简单假设是无效的。举例来说，假设一个z方向的传导波有z、t的函数
，其中 在电介质及空气中是相同的，则纵向的横截分解为：
特别的是y分量：
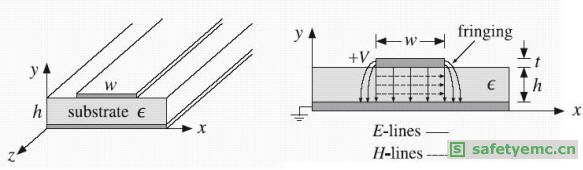
图五：微带线
边界条件需要分量
及
，它们不断地穿过电介质与空气的接口。其条件如下：
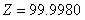
结合此两个条件，可得到：
审视图五中的边缘型态，我们注意到电场在空气中有非零的x分量
。因此，上式的左边不可以为零，且电波不可以假设为标准的TEM。
然而，可以假设
在空气及电介质中都不大，因为横向电场的主要方向是在y轴。这会产生所谓的「准TEM（quasi-TEM）近似」现象，电波被假设为近似TEM，且来自TEM的偏差效应，会被线路阻抗及速度系数的经验公式纳入计算。
尤其是，使用一个有效的电介质均匀地充填整个空间，以取代空气与电介质的接口，这就是一个TEM传导模式。若我们以
符号表示有效电介质的相对「介电常数（permittivity）」，则线路的波长与速度系数将可用其自由空间的值
、来表示：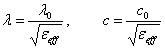
有许多现存的经验公式，是关于线路的特征阻抗及有效电介质常数。Hammerstad与Jensen的公式是其中最精确者之一：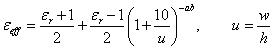
（19）
是电介质的相对介电常数，而a、b的量被定义为：
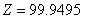
这些公式的精确度在
时，大于0.01%；在
时，大于0.03%。同理，特征阻抗的经验公式为：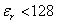
（20）
，且函数
被定义为：
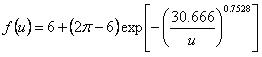
其精确度在
，且时，大于0.2%。在
比率到达最大极限或时，方程式（19）和（20）有变成平行平板线的倾向：
一些常见的基板层电介质材料被应用于微带线中，它们包括：
1. 矾土（alumina）：是一种具有陶瓷外型的氧化铝（Al2O4），
。
2. 2.RT-Duroid：是一种铁氟龙（teflon）复合材料，
。
宽度与高度的实际比率是在之间，而特征阻抗的实际值是在10~200欧姆之间。表一分别显示了在与两种情况下，Z与
在u上的关系。
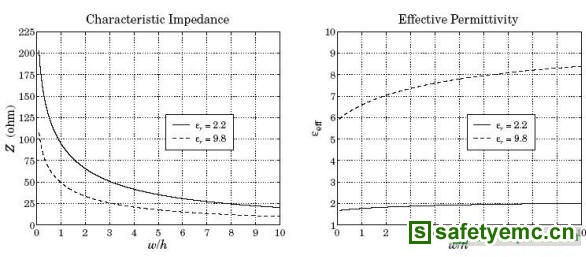
表一：微带线的特征阻抗和有效介电常数
微带线的合成需要先决定
比，以得出一个特定的特征阻抗Z。方程式（20）的逆向计算（以Z来解u）是不可行的，直接合成的经验公式是存在的，但并不像方程式（20）那样精确。假定一个想要的Z值，假设
，
可由下式计算：
（21）
若时：
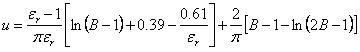（22）
这里的A、B是：
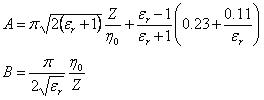
这些公式的精确度大约是1%。这方法可透过反复的改良过程，以达到实质上与方程式（20）一样的精确度。从方程式（21）、（22）计算u开始，Z的值是由方程式（20）计算。如果Z大于线路阻抗要求值的0.2%的话，则u需做轻微的改变，直到精确度达到要求的水平。因为Z是随着u做单调递减的，如果Z小于要求值，则将u降低少量的百分比，反之，则将u增加少量的百分比。
MATLAB的三个函数mstripa、mstrips、mstripr可分别执行分析、合成与改良过程。它们的使用方式为：
[eff,Z] = mstripa（er,u）; % 分析方程式（19）与（20）
u = mstrips（er,Z）; % 合成方程式（21）与（22）
[u,N] = mstripr（er,Z,per）; % 改良
