表2第一组模型感应电压Uz的波形参数
| 模型号 | 天线极板边(cm) | 峰值(V) | 上升时间(nS) | 脉宽(nS) |
| 1 | 8 | 783 | 2.4 | 24 |
| 4 | 6 | 750 | 2.4 | 24 |
| 5 | 4 | 728 | 2.4 | 24 |
(2)保持正方形天线极板的边长不边,均为8cm,改变天线极板到内部接地体的距离,当三维天线的z极化方向与入射波电场极化方向一致时,Uz的计算结果见表3。 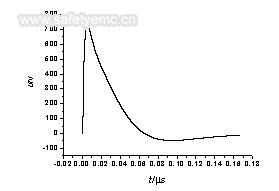
图4三维天线z方向感应电压z时的域波形
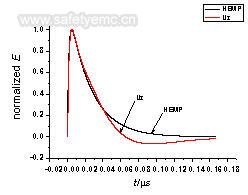
图5入射场波形与Uz归一化波形比较
表3第二组模型感应电压Uz的波形参数
| 模型号 | 距离长度(cm) | 峰值(V) | 上升时间(nS) | 脉宽(nS) |
| 1 | 1 | 783 | 2.4 | 24 |
| 2 | 0.5 | 399 | 2.4 | 24 |
| 3 | 1.5 | 1145 | 2.4 | 24 |
(3)为了研究改变导电立方体尺寸对三维测量带宽的影响,也设计一组计算模型,模型的结构参数及数值模拟的统计结果见表4。可以看出,接地极的边长的改变对天线的频率响应影响很大。
表4 仅改变接地体尺寸时的计算模型参数及天线频率响应数值仿真结果
| 序 号 | 计算模型参数 | 频率响应 | ||
| 接地极的边长(cm) | 天线极板至接地极的距离(cm) | 极板边长(cm) | 感应电压的3dB带宽(MHz) | |
| 1 | 9 | 1.5 | 4 | 816 |
| 2 | 7 | 1.5 | 4 | 1010 |
| 3 | 6 | 1.5 | 4 | 1153 |
| 4 | 5 | 1.5 | 4 | 1376 |
| 5 | 4 | 1.5 | 4 | 1800 |
3. 结论
(1) 从数值模拟结果上来看,保持天线平板到内部立方体的距离不变,只改变正方形平板的尺寸大小,对感应电压影响不大;保持正方形平板的尺寸不变,改变平板到内部立方体的距离,对计算结果有很大影响,距离增加一倍,感应电压的峰值近似增加一倍。
(2)从感应电压的波形看,三维天线的高频响应很好,低频响应不足,需要在实际设计时对低频进行补偿。
(3)接地极的边长的改变对天线的频率响应影响很大,接地极的边长减小可以提高天线的带宽。
参考文献
[1] K. S. Yee, “Numerical solution of initial boundary value problems involving Maxwell’ equations in isotropic media, ”IEEE Trans. on antennas Propagat, vol.14, no.4, pp. 302-307,1966.
[2] 王长清,祝西里,“电磁场计算中的时域有限差分法”,北京大学出版社,1994.
[3] A. Taflove, Computational Electro- dynamics – The Finite- Difference Time- Domain Method, Artech House, 1995
[4] J. Berenger, “A perfectly matched layer for the absorption of electromagnetic waves,” J. Comp. phys.,
Vol.114, no.2, pp.185-200, Oct. 1994.
[5] B. Chen, D. G. Fang and B. H. Zhou, “Modified Berenger PML absorbing boundary condition for FDTD meshes”,
IEEE Microwave and Guided Wave Lett., Vol.5, no.11, pp 399-401, Nov. 1995.
[6] A. Taflove, and M. E. Brodwin, “Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell’s equation”,
IEEE Trans. on Micro-wave Theory Tech., MTT-23, pp. 623-630, 1975.
3.2 入射设置
计算中采用高空核爆炸(HEMP)的标准波形,假设照射到三维传感器的均为均匀平面波。
HEMP入射波电场为:
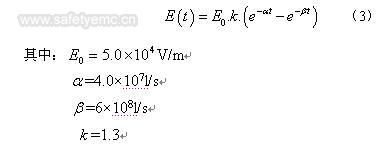












 苏公网安备32050802011615号
苏公网安备32050802011615号