2 耦合模型电路参数的提取

　　由于不同结构、不同敷设方式、不同材料的电缆的电容矩阵[C]和电感矩阵[L]都不相同，计算互连电缆间电磁耦合量时必须准确地提取模型的电路参数（单位长度的电导矩阵[G]、电阻矩阵[R]、电容矩阵[C]和电感矩阵[L]等）。由于单位长度传输线间的电导与传输线横向间阻抗相比可以忽略，即[G]＝0，同时考虑传输线的实际电阻相对较小，为简化预测模型，我们假设电阻矩阵[R]＝0。因此，通常不予考虑[R] 和[G]，在多导体传输线系统的模型中只考虑[L] 和[C]。

　　本文采用电磁场有限元的数值方法，通过求解静电场问题得到传输线的电容矩阵[C]，则传输线的电感矩阵[L]可由式(6)求得：

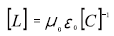　　（6）。

　　其中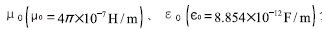，分别为自由空间的磁导率和介电常数。

　　通过对多导体传输线系统的电容矩阵和电感矩阵的提取计算，可以建立耦合模型的LC等效电路。当传输信号为低频时，我们可以采用简化的集中参数模型进行电路仿真分析。这种简化模型此时可以得到足够的精度。

　　但高频传输时我们必须采用分布参数模型，将信号传输线沿长度方向分为n段，把这n段LC电路级连起来得到整条传输线的等效模型。最后，对电路模型用SPICE进行仿真，得出其他导线的电磁耦合量。

3 数值结果分析

　　在电子设备中,各模块间的数据传输通常采用扁平电缆。以下对扁平电缆在不同的导线间距时的线间串扰进行预测分析。

　　该模型的结构参数为：两导体的半径r＝0.0004m，绝缘层厚度t＝0.0004m，耦合线长l＝1m。互连电缆串扰预测的频率范围为100kHz～100MHz。我们采用集中参数的等效电路进行仿真分析。在四种不同的导线间距情况下，用有限元方法提取的等效电路参数如表1所示。

　　表1 不同导线间距电缆的等效电路参数

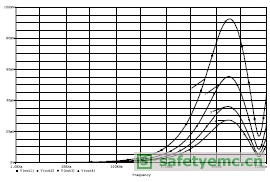
　　图5 不同导线间距电缆电磁耦合响应曲线