3 混合基函数的构造
图 2（a）表示定义在三角形面元对上的基函数，具有如下形式^［3］：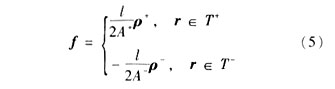

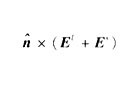
文献［12］给出的一次参数曲面上的线性基函数定义在图2（b）所示的四边形面元对上，其函数形式为：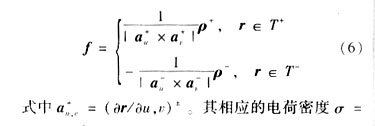


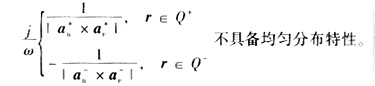
该式表明，当四边形网格的某一条边特别短时，该边附近的电荷密度就会很大，这是不符合实际情况的，在计算时会带来误差。但是在对自由曲面的纯四边形网格剖分以及用四边形处理天线与载体连接处基函数时，这个问题不可避免(参见图3(a))。

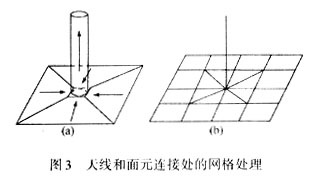
当四边形网格中存在含有特别短边的四边形或者三角形时，虽然式(6)描述的传统的基于四边形网格的基函数仍然可以用于计算，但是模拟结果却不准确。文献［12］详细描述了在四边形网格剖分质量变差的情况下模拟表面电荷分布时存在的不足（文献［12］之图4），指出可以使用高阶基函数来解决这一问题。但是采用高阶基函数会带来计算上的复杂度。我们认为，当四边形面元中最长边与最短边之比超过20时，可以通过网格优化算法将短边缩成一点，将此面元退化成三角形。在新的网格中，四边形或者三角形的质量都是好的。此时在不同种类的面元上采用不同的基函数，则可避免在三角形面元上产生不正确的电荷分布。

图2（c）表示1个三角形和1个四边形组成的面元对,在其上建立混合基函数：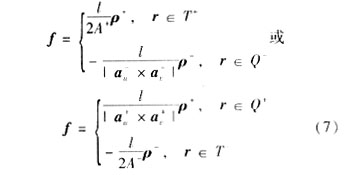

式中四边形部分相比式(6)增加了系数l（公共边长度），以使新的基函数具有局部连续性^［12］，且在整个面元对上电荷总量为0，即不引入虚假电荷。使用混合基函数不但能解决上述电荷分布模拟的精确度问题，而且由于在同样的剖分密度下，所需四边形的个数比三角形少，采用混合基函数能同时兼顾到具体目标的网格剖分质量和密度，从而可引入更少的未知元。目标表面经过剖分后，某处究竟采用何种基函数取决于位于此处的边所连接的两个多边形的形状。