功率损失、电阻与电导

 假定在最佳传导状况下，计算场型（field pattern）与特征阻抗。因电介质及导体的电阻发热所造成之损失，可用传输线的另两个特征常数来量化，也就是每单位长度的电阻与电导。导体与电介质损失所导致的衰减系数：和，是用、及Z来表示：
（13）
它们可由下面的一般项式导出。是在导体壁上的感应表面电流，这里的是到导体壁的向外法线。

利用BAC-CAB法则，可得出。但是，在导体A的表面上是平行于的，而在B上则是不平行的。因此。此结果产生了，其在A上指示着+Z的方向，而在B上指示着方向。利用这些式子，可得出导体的每单位z长度之功率损失为：
（14）
因为而与总电流I相关（见方程式（8）），因此可用来定义每单位长度的电阻：
（导体欧姆损失） （15）
利用方程式（11），得出衰减系数为：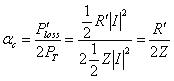
（16）
如果导体间的电介质是以导电率或损失切线做轻微的传导，则将会有一些电流在两导体之间流动。

每单位z长度的感应并联电流是与电导相关，。电介质中的并联电流密度为。由导体A流向导体B的总并联电流，是沿着导体A的圆周对做积分求得：

利用方程式（9），可得出：
 
此结果产生的电介质损失常数将为：
 
或者，因并联电流产生的每单位长度之功率损失将为，因此可用下式来计算：
 
一般在实用上都以损失切线与波数，来表示电介质的损失和并联电导：
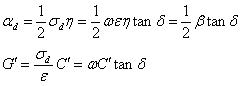（17）
上面已经将RF传输线的原理和特性，详细地探讨完毕。底下我们将讨论三个应用实例：平行平板线、微带线、同轴缆线。在每个例子中，我们会讨论其先天的静电问题，及求得特征阻抗Z与衰减系数和。

平行平板线

在图四中，平行平板线是由两个宽度w的平行传导板所组成，这两个平板之间是以电介质材料分开，间隔（高度）是h。像是在微波集成电路里，所使用的微带线就是属于这种线路。
　
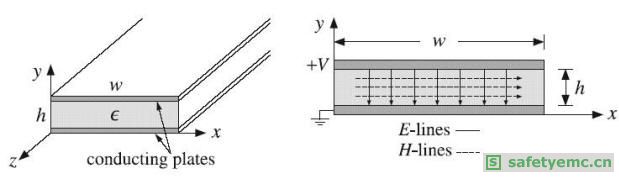
图四：平行平板线

由于w与h的值是多变化的，因此在平板末端的边缘效应是不可以被忽略的。事实上，边缘需要电场来拥有纵向的分量，因此严格来说，它并不支持TEM模式。

然而在假设宽度远大于高度时，可以忽略边缘效应，并假设电场是独立于x坐标的。

此静电问题是等效于一个平行平板电容器。因此，此电场将只有y分量，且在平板之间是不变的。同理，磁场将只有x分量。经由方程式（7）与（8）：
 
因此，线路的特征阻抗将为：
 
在上式中，我们使用。经由方程式（10）所推得的传输功率为：
 
经由方程式（5）所推得的每单位长度之电感与电容为：
 
在导体顶部的表面电流为，在导体底部则为。因此，每单位z长度的功率损失为：
 
与方程式（15）相比较，我们确认每单位长度的电阻为。因此，由导体损失所产生的衰减常数为：
（18）