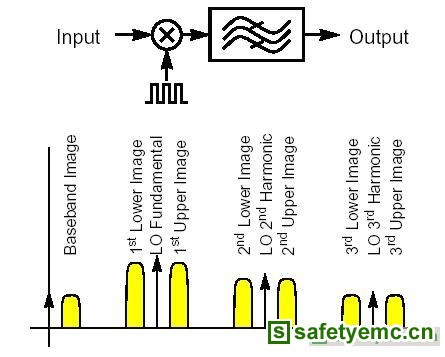
如附图三所示，在非线性电路中传送窄频讯号时，会产生一个频谱相当稀疏的宽带讯号。一般来说，此频谱是由靠近载波附近的谐波频率丛集（cluster）而成的。如果调变是周期性或准周期性（quasiperiodic）的，则这些丛集是频率的离散形式；不然，它将是频率的连续分布。

射频仿真软件可以利用此频谱的稀疏特性，在不同状态下，得到真实的模拟效果。当频谱是离散时，「稳定状态（steady-state）法」会被使用；当频谱是连续时，瞬间分析法会被使用。

*射频讯号路径随时间变化的线性特性

射频电路另一个重要但较少被查觉的特性是：从输入端到输出端，它们一般都会被设计成线性的电路，以避免调变或信息讯号的失真。一些射频电路，譬如混合器，是用来将讯号从一个频率转换至另一个频率。其实，它们是被一个额外的讯号LO驱动着，LO是一个大的周期性讯号，其频率是进行频率转换时所需要的。为了能得到最佳的效能，混合器被设计成可以用很强的非线性方式来响应LO。因此，混合器同时具有近似线性（至输入）和强大的非线性（至LO）特征。

产生时序（timing）或频率（clock）的电路，例如：LO，是和信息讯号无关的，因此，它可以被视为混合器的一部份，而不是混合器的外部（输入）电路，如附图四所示。这种观念上的简单改变，可使混合器具有单一输入讯号和一个近似线性、随时间变化的周期性转换函数（transfer function）。例如：有一个混波器是以一个理想的乘法器制成的，它后面跟着一个低通滤波器。乘法器是非线性的，并具有两个输入讯号。当一个LO讯号cos（）取得一个输入讯号之后，会产生一个转换函数值 ：
= LPF{ cos（）}

从上式清楚可知，是随着时间变化的，并且与成正比例的关系。如果输入讯号是：=，那么：= LPF{}=
上式表示一个线性周期变化的转换函数实现频率转换的功能。
　
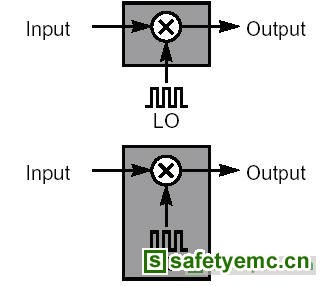
图四：将LO视为混合器的一部份
　
通常我们会假设信息讯号很小，因此，可以将输入端到输出端之间的电路功能当成近似于线性。只要小讯号分析可以解释讯号路径的周期性变化特性，就可以进行小讯号分析。这是在接近周期发生的工作点上，进行线性仿真达成的。传统的仿真软件，譬如SPICE，支持许多小讯号分析工具，例如：交流和噪声分析，这些工具在分析放大器和滤波器时，是很有效用的。然而，它们是在接近固定的工作点上， 对非线性时间不变的电路，开始进行线性仿真。因此，会产生线性时间不变的函数，但是无法代表频率转换的效果。

在一个周期变化的工作点附近，对一个非线性电路进行线性仿真，致使小讯号分析能够延伸应用到频率电路上，或者需要周期性频率讯号的电路上（此周期性的频率讯号可以让电路正常地工作），例如：混波器、交换式滤波器、取样器、和振荡器（由于振荡器是自行计时运转，所以频率讯号是振荡器的输出。信息讯号通常是不需要的讯号，譬如噪声）。若是如此，就会产生周期性变化的线性函数，而且，它的确能代表频率转换的效果。