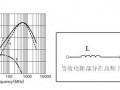
例如，下述的无源器件就可以用这种方法来表征，在１５０ｋＨｚ到３００ＭＨｚ频率范围内的电感Ｌ _１（３ｍＨ）与Ｌ_２（４００μＨ），电容Ｃ_１（４７ｎＦ）、Ｃ_２（２２０ｎＦ）与Ｃ_３（１μＦ，聚酯型）。应使用合适的插入损耗方法，即在分析频率上，阻抗大于１００Ω的电感以串联插入来表征，而阻抗小于２５Ω的电容以并联插入来表征。电感的结果参见图２，电容的结果参见图３。

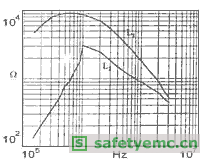
图２　电感Ｌ_１和Ｌ_２高频阻抗的测试结果 

 

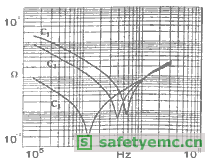
图３　电容Ｃ_１、Ｃ_２和Ｃ_３高频阻抗的测试结果

电感Ｌ_２曲线上有一个由于点的数量有限而产生的折线角；在任何情况下，器件均有一明显的非理想特性。
　　还观测到，由于寄生串联电感的影响，三个电容在１００ＭＨｚ以上的阻抗是相同的。这一现象很有意思。这意味着，如果将其用作高频滤波器，将会得到相同程度的衰减。之所以如此是因为，在这个频率范围内，由于外部连接器的存在，串联寄生电感占主导地位。

２.２　寄生参数的确定
　　从被测阻抗除去这些无源器件的寄生参数值，就可以得到无源器件的等效电模型。一个工作频率能达到高频的无源元件的有效模型是很有用的，它有助于理解元件置入复杂电路后产生的影响，也有助于从电路仿真中得到可靠的结果。
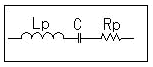
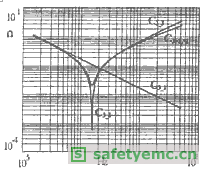
　　图４a说明，该电模型可表示电容Ｃ_３，其中Ｌp和Ｒp分别代表串联寄生电感和电阻（不考虑与模拟介质损耗的电容Ｃ相并联的电阻，因为它的作用只会在低的频率下体现出来）。图４ｂ示出了模型中每个寄生元件的影响：Ｃ_３－１代表了模型中参数Ｃ的值，这个值通过前述特性阻抗（图中表示为Ｃ_{３ＲＥＡＬ}）的低频渐近线可以很容易地确定；Ｃ_３－２代表的是考虑了串联电感Ｌｐ相同的电容，其串联电感的值可以通过高频渐近线来估计；最后，观察到的被测电容阻抗的谐振峰值可以来确定串联寄生电阻Ｒｐ，它由标着Ｃ_３－３的完全模型阻抗曲线示出。如前所述，确定的寄生元件值就可给出电容实际性能的满意的近似值。

（a）

（b）

图４a）　Ｃ_３的等效电模型