2    实例分析

    LC滤波器和四阶直流线路滤波器是工程实际中常用的滤波器,下面就以上面的结论分析其滤波效果。图4为LC滤波器原理图。

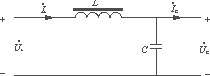
图4    LC滤波器原理图

    其混合参数方程为

（2）

    对于直流分量，由于f趋向于0，对应有ω=2πf趋向于0；显然g11=g22=0；g12=g21=1。

    对于谐波分量，

    |g11|=；|g12|==|g21|；|g22|=。

    考虑到当ωL>10时，显然有g11=g12=g21=g22=0。分析系统的输入导纳和输出阻抗，要保证输入导纳g11趋向于0，必然使得L取值很大；要保证输出阻抗g22趋向于0，必然使得C取值同样很大，这给工程实际应用带来了局限性，这也正是LC滤波器的缺点。

    在工程实际中广泛应用的四阶直流线路滤波器其原理图如图5所示。

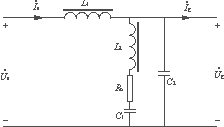
图5    四阶直流线路滤波器原理图

    其混合参数方程为

（3）

式中：

    g=。

    如果令z=，则可以求得相应的参数如下：

    g11=gz；g12=g21=z；g22=－L1sz。

    下面分析此滤波器电压传递函数的幅频特性，滤波器的电压传递函数为

    G(s)==（4）

    将参数g代入，应用MATLAB做出其对数幅频特性曲线如图6所示。

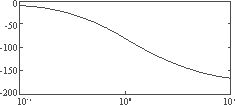
图6    系统的幅频特性曲线

    显然，在低频段输出电压的衰减较小，高频段的滤波效果比较明显。

    由以上分析可以看出，由于此电路元件参数的选择范围较宽,因此较容易设计出满足设计要求，且适用于工程实际的滤波器。作者已将此电路应用到了为长沙某公司所设计的开关电源中。