共模转差模传递函数

图6展示了一个共模转差模电路分析的等效拓扑结构：桥式电路。

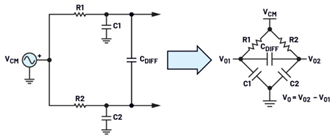
图6.用于共模转差模电路分析的电路拓扑结构。

自十九世纪中叶以来，桥式电路（例如惠斯通电桥）就已得到了广泛应用。尽管桥式电路在众多领域都有应用，但它在这里用作一种分析工具。图7着重展示了通用桥式电路的传递函数方程（由惠斯通电桥推导扩展而来）。

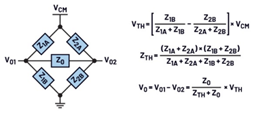
图7.桥式电路（惠斯通电桥）。

将这些公式应用于图6中的电路，可得到以下共模至差模转换的传递函数：

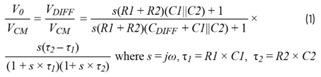
请注意，这个传递函数有三个极点和两个零点。从系统工程的角度来看，这是一个3阶1型系统传递函数。公式2展示了通用的公式形式，突出了电路不平衡的影响（即当 τ2 ≠ τ1时）。

令人惊讶的是，对于仅有五个无源元件的情况而言，这个包含五项的传递函数相当复杂。研究各个单独的项有助于深入了解如何进行可能的简化。极点p1和p2将确定两个较高的频率转折点，而极点p0将确定一个较低的频率转折点。默认情况下（由于存在额外的电容），BWp0 < BWp1 ≈ BWp2。如果采用了较大的CDIFF (CDIFF >> C1||C2)，则较低频率（即低于BWp0）的共模噪声传递对于C1和C2的不匹配将变得不那么敏感。

实用共模转差模传递函数近似值

参考图5中的带宽近似值，请注意，极点p1和p2与共模带宽相对应。此外，如果R1≈ R2且C1≈ C2，极点p0则与差模带宽相对应（具体推导过程留给读者自行完成）。

进一步来看，如果R1≈ R2且C1≈ C2，零点Z1近似等于两个极点p1和p2中的任意一个。消去一对近似相等的极点/零点，不仅会简化我们的表达式，还能得到一个实用的传递函数近似值。

被消去的这对极点/零点在低频时不会影响共模转差模的增益。在高频情况下（对于调幅(AM)无线电发射而言，频率≥535 kHz时），根据EMI滤波器的不匹配程度，它确实会带来一些增益误差。

近似的共模转差模转换传递函数为：

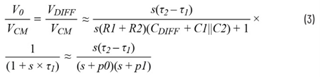
注：表达式中保留了极点p1，假定它与极点p2相比设定了一个更高的转折频率。这个极点对更高频率的衰减会有更大的影响。

对公式3进行分析可以发现，当分子中的两个时间常数相等时，电路处于完全平衡状态，此时传递增益为零（即具有无限大的共模抑制能力）。虽然从理论上来说这是可能的，但在实际中这种情况非常罕见。即便有人手动对电路进行平衡调节，诸多其他因素（诸如元件老化、温度变化、电压影响等）仍会致使电路偏离这种理想状态。对设计人员而言，应当投入更多时间来了解共模转差模转换对元件容差的敏感程度。这将有助于为共模电磁干扰噪声设定初始的抑制级别。

注：共模转差模EMI滤波器通常不被视为精密电路。它应用于环境噪声信号强度不太明确的情形。正因如此，它旨在帮助抑制常见的已知噪声源（例如电力线干扰、调幅无线电干扰等）。

在跨越了“无限之桥”后，让我们回到现实世界，要明白，电路不平衡才是常态。实际上，我们关注的重点正是最坏情况下的电路不平衡状态。重新审视公式3，请注意，该传递函数以20 dB/dec的速率上升，在低频极点(fL)处趋于平缓，然后在高于高频极点(fH )的频率段以-20 dB/dec的速率下降。中心频率可以通过取两个极点频率的几何平均值来近似计算。然而，这种近似计算的误差会随着元件失配程度的增加而增大。对于较大的失配误差（例如，容差为±1%的电阻和容差为±20%的电容），建议（通过手动分析和/或仿真的方式）找出在相移为-180°时的峰值增益。

峰值中频增益的近似计算方法如下：

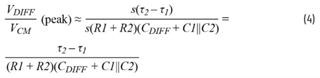
如果CDIFF >> C1 ≈ C2，则峰值中频增益可以进一步简化，如下所示：

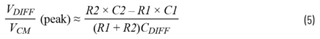
如果对所有元件都选择用δ表示的相同容差，公式5可简化为：

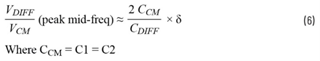
虽然从设计的角度来看，这（选择具有相同容差的元件）在某种程度上具有一定的局限性，但它强调了一个要点，即电容比（共模电容与差模电容之比）越小，电路对共模噪声的衰减能力就越强。

回到公式5，在分析电路在最坏容差条件下的情况时，假定元件的值是有偏差的，使得分子达到最大值。RC时间常数的失配（电路不平衡）越大，共模噪声就会更多地混入差模通道中。将注意力转向分母项，注意到电阻之和简单来说就是标称电阻的两倍，表达式可以简化如下：

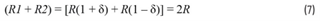
把公式7代入公式5，得到：

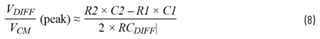
公式8是一个非常简单且实用的共模转差模转换中频增益的近似公式：即共模时间常数失配值除以标称差模时间常数。只要CDIFF很大（CDIFF ≥ 100 × （C1和C2的值）），公式8就相当准确。

有人可能会想随意增大CDIFF的值，以降低分子（即电阻电容时间常数失配）的敏感度。遗憾的是，这种做法是受限的，因为它会设定差模通道的带宽（也就是我们所关注的信号的带宽）。因此，需要进行权衡取舍。

现在，可以利用峰值中频增益以及低频和高频转折频率，来近似估算在 50 Hz/60 Hz（潜在电力线干扰）和535 kHz（潜在的AM无线电频谱干扰的低频端）时的共模抑制能力。下面的例子着重说明了这一点。