共模转差模传递函数示例
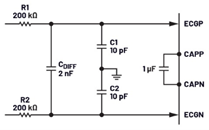
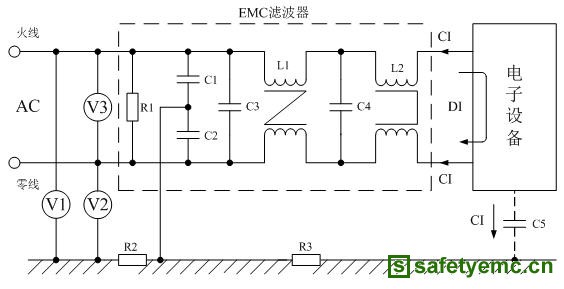
图8.EMI滤波器示例。
我们假设每个元件都有0.1%的容差。这将提供一个参考水平,以便与其他EMI滤波器电路场景进行比较(见图8)。对于最坏情况(wc)下的抑制近似计算,请使用以下数值:
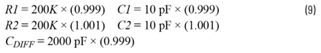
应用公式8:
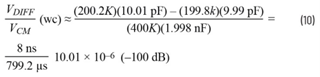
请注意,前面表达式的分母是低频转折频率的时间常数,我们可以很容易地计算出fL:
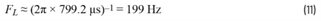
现在使用较小的RC时间常数来确定较高频率的极点:
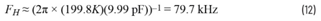
有了这些数值,我们现在可以按如下方式估算在50 Hz/60 Hz和535 kHz时的衰减:
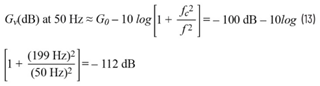
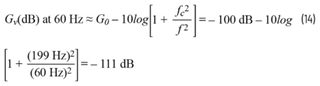
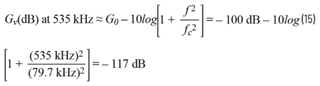
这些手动计算结果与电路仿真结果非常吻合(见图9)。请记住,这并不是一个精密电路。对于EMI滤波器的应用来说,几分贝(dB)以内的近似值通常是可以接受的。
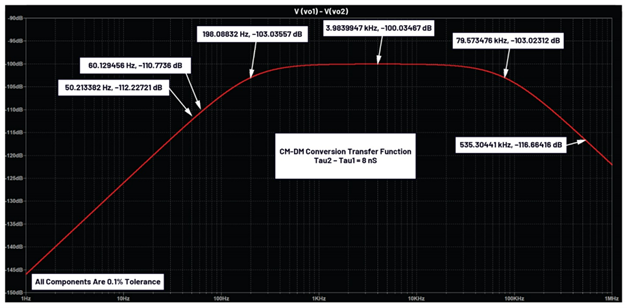
图9.使用容差为0.1%的元件对EMI滤波器进行的LTspice仿真。
表1重点显示了该电路在50 Hz/60 Hz和535 kHz频率下,针对不同元件容差水平的共模转差模抑制能力。第一种情况(容差为±0.1%)在某种程度上是一个任意参考点,基于在实验室工作台手动测量无源元件而设定。其他情况则反映了市面上常见的电阻和电容的容差水平,以便进行比较。
表1.EMI滤波器共模转差模衰减估算
最坏情况下共模转差模的衰减估算
| 抑制能力估算(公式4 - 手动计算) | EMI滤波器衰减(LTspice仿真结果) | |||||
| 场景 | Gv (dB) / 50 Hz | Gv (dB) / 60 Hz | Gv (dB) / 535 kHz | Gv (dB)/50 Hz | Gv(dB) / 60 Hz | Gv(dB) / 535 kHz |
| 所有元件0.1% | –112.3 | - 110.8 | - 116.6 | - 112.3 | - 110.8 | - 116.7 |
| 所有电阻1%; 电容0.1% | - 97.5 | - 96.0 | - 101.7 | - 97.4 | - 96.0 | -101.9 |
| 所有元件1% | - 92.3 | - 90.8 | -96.4 | - 92.2 | -90.8 | -96.6 |
| 所有电阻1%; 电容5% | - 82.7 | - 81.2 | - 86.2 | - 82.7 | - 81.2 | - 86.7 |
| 所有电阻1%; 电容10% | - 77.4 | - 75.9 | - 80.0 | - 77.4 | - 75.9 | - 81.0 |
| 所有电阻1%; 电容20% | - 71.7 | - 70.2 | - 72.3 | - 71.7 | - 70.2 | - 74.3 |
抑制能力估算(公式4 - 手动计算)
EMI滤波器衰减(LTspice仿真结果)
请注意,在进行最坏情况的估计时,RC时间常数的容差会翻倍。也就是说,如果差模电路的一侧增加X个百分点,另一侧可能会减少X个百分点。例如,如果R1和R2是容差为1%的元件,C1和C2是容差为10%的元件,那么最坏情况下的RC时间常数失配率为22%。与容差为0.1%(即时间常数失配为8 ns)的参考情况相比,440 ns(22%)的失配会使共模抑制能力降低35 dB。这无疑是相当大的损耗!至于这种损耗能否被接受,需视具体使用场景而定。
图10展示了共模抑制比与Delta Tau的关系曲线,其中Delta Tau表示RC时间常数失配量。在底部横轴旁,几个对应的RC容差水平以红色标注。为作说明,64 ns Delta Tau水平对应于1.6%的RC容差(64 ns/2 µs = 3.2%最坏情况失配 = ±1.6%RC容差)。从该曲线图的斜率可知,每当RC时间常数失配量翻倍时,共模抑制比就会降低6 dB。
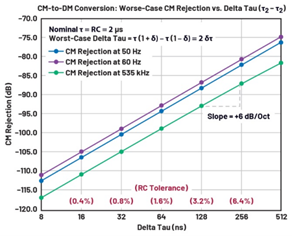
图10.共模抑制与Delta Tau(τ2– τ1)
要点总结
• 预测并验证电磁干扰(EMI)环境。
• 等效的共模转差模电路是一种桥式电路,属于非线性电路。
• 通过合理选择CDIFF,设计人员能够利用公式8及计算得出的转折频率,轻松估算共模转差模的转换情况。
• 增大CDIFF的值,会降低电路对C1和C2之间失配的敏感度,也会降低对Delta Tau(即共模RC时间常数失配)的敏感度。
• 根据一阶近似,每当RC失配量翻倍时,共模抑制比就会下降6 dB。
• 元件制造容差只是其中一个影响因素。温度、电压以及元件老化也会对元件之间的失配产生影响。
• 所有的计算都是基于最坏情况下的失配进行的。其他任何情况只会使电路性能更好,最终达到理想的无限大共模抑制比。
• 分析并理解所用的电路,找出性能方面的权衡取舍及适用的近似计算方法。不要仅仅依靠仿真来进行设计。
• 这种分析方法可以扩展应用到AAF的设计中。








 苏公网安备32050802011615号
苏公网安备32050802011615号