电波是由相互垂直的电场（Electric Field）与磁场（Magnetic Field）组成。两者交互变化的强度取决于输至传输线（transmission line）或天线上的交流信号之大小而定。如图一所示。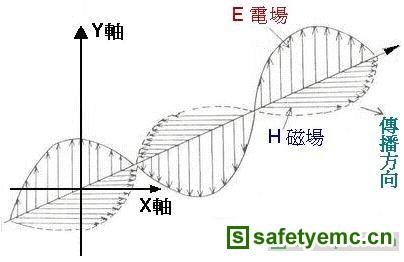
　
图一：电波的组成

若依传导（propagation）方向与电场或磁场的关系，可以将电波分成三大类：横向电磁波（Transverse Electromagnetic Wave）或简称TEM波、横向电波（Transverse Electric Wave） 或简称TE波、横向磁波（Transverse Magnetic Wave） 或简称TM波。横向电磁波的定义是，电波的传导方向上没有电场和磁场的成份，电场和磁场的变化方向是在与传导方向垂直的平面上，所以又称为「平面电磁波（Plane Wave）」，图一就是一个典型的平面电磁波。

横向电磁波传输线的一般特性

TEM波模式是由下面方程式来描述，而后两者可用来描述等效的二维静电问题：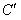
（TEM模式） （1）
上述方程式中的第二式暗示着 可表示二维静电电位之能量梯度。因此第三式变成拉普拉斯（Laplace）的电位方程式。如此则电场可由下面的方程式取得：
（等效静电问题） （2）
因在静电问题中，电场线必须始于正电荷导体并结束于负电荷导体，所以TEM模式只能在同轴缆线或双芯线（two-wire line）等多导体中被传导。中空的（hollow）波导（waveguide）并不支持TEM模式。

图二是一个双导体传输线的横向截面积。此截面的外形是任意的。

图二：双导体传输线

在静电的解决方案中，这些导体是等电位的（equipotential）。设、为两个导体上的电位常数，则导体间的电压差为。电场线会垂直导体（a）出发并垂直于导体（b）结束。

被认定为等电位线的磁场线，根据方程式（1），垂直于电场线。磁场线本身彼此包围着，并围绕着两个导体。

特别是在导体表面上，磁场是正切的。根据安培定律，每个导体周围磁场的线积分，会在导体的沿z方向，产生流动的总电流与，这两个电流是大小相等、方向相反的。

阻抗、电感与电容

因为电波是沿z方向传导，频率为、波数（wavenumber）为，电压V与电流I的z、t函数为：
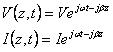（3）
针对后向移动的电压及电流波，我们必须以取代。的比率维持不变且独立于z。这便是线路的特征阻抗（characteristic impedance）：
（线路阻抗） （4）
除了阻抗Z外，TEM线路的特征还有每单位长度的电感及电容。就不会产生损失的线路而言，这三个量Z、、的关系如下：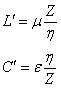
（每单位长度的电感及电容） （5）
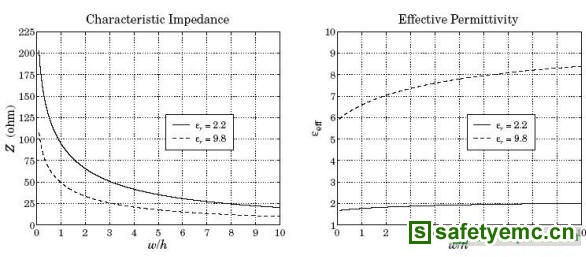
此处的是两导体间电介质的特征阻抗。利用与的相除与相乘，可以得到下列关系：
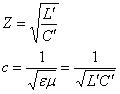（6）
线路的速度系数是的比率，这里的是电介质的折射率，此电介质是假设不具磁性的。

因为，所以导波波长为，此处的是自由空间（free space）之波长。对传输线的有限长度l而言，代表线路的电气长度（electrical length），和薄膜（thin-film）层中的光学长度（optical length）扮演相同的角色。

方程式（5）与（6）的结果适用于任何的TEM线路。从图三中可导出这两个方程式。

在图三中，延着由A至B的任意路径对做积分，可求得电压V。然而，若选择的路径为E场线，则，且Ｖ为：
（7）
同理，延着围绕A的任何封闭路径，对做积分可求得电流I。若选择的路径为H场线，例如导体的圆周，我们将得到：
（8）
导体A的一个无穷小区域上的表面电荷为，这里的是表面电荷密度。因为导体是假设为理想状态，则边界条件的要求为等于D场的法线分量，亦即。则。
 
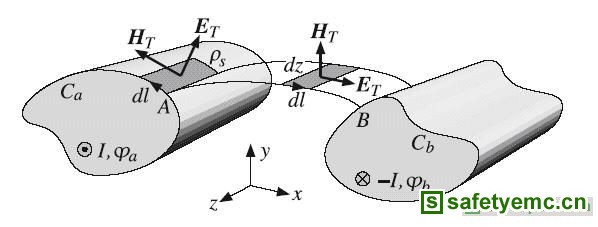
图三：电荷和磁通量

若沿整个导体A的圆周做积分，将会得到每一单位z长度的总表面电荷：
 
但由方程式（1）得到的关系式，及利用方程式（8）之结果，可以得到：
（9）
因为与每单位长度之电容和电压有关，所以可得到：
 
接下来，考虑两导体上的点A、B之间的E场线。因为向量是与此区域垂直的，所以通过无穷小区域的磁通量（magnetic flux）为。

若由A积分到B，则连结两导体的每单位z长度之总磁通量为：

以 来取代，并利用方程式（7），可得出：
 
由
 

因为磁通量与电感的关系是。因此：
 

传输功率

Z、、之间的关系也可用能量的考虑来导出。延着线路传输的功率（transmitted power），是由将线路横截面S上的Poynting向量之z分量积分得到的。在TEM模式下，，所以：
（10）
方程式（10）在一般表示时，都会重写成：
（11）
在本文最后会例出几个实例来验证上述的方程式。利用下面的Green等式也可证明：
 
因且，可得：
 
则二维的高斯（Gauss）定理暗示了：
 
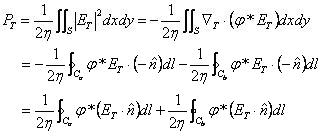
这里的是到导体的向外法线（是由区域S向外的法线）。因导体是等电位表面，所以在导体A上，而在导体B上为。利用方程式（9），且在导体A与B上，，则可得：
 
沿着此线路的电磁能量分布，是以每单位长度在平均时间内的电能与磁能密度来描述：
 
利用方程式（10），可将上式重写成：
 
因此，且总能量密度为，这暗示了能量速度将会是。我们也可以利用线路的电容及电感来表示能量密度：
（12）