此效应可以藉由增加取样频率作某种程度的消除，但这也会造成影像在频率上展开得更宽，而且要对需要处理的取样数量增加进行取舍。然而在某些应用上，这仍是一种可接受的取舍。此范例也强调讯号路径中的滤波以限制在 ADC 输入端的频道外噪声的重要性。 

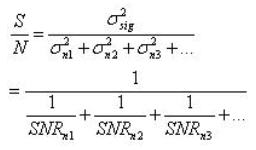
下一部分会检视如何结合数个噪声来源的效应表示为频率抖动的公式，以了解不同的来源的影响并且定义一个频率抖动上限。此范例会结合热噪声、量化噪声与取样频率相位噪声。如果假设各个这些噪声来源彼此是独立且不相关的（合理的假设），则复合的 SNR可以表示为下式：

（3）

虽然常认知的SNR是在对数单位下所表示，但注意上式的每项都是以线性单位表示的数值。在第一式中使用变异数的表示法来强调处理随机过程，它甚至可以包含所需的讯号。

为了找出各噪声源的SNR，从热噪声开始。出现在特定的固定频宽 Df 中的热噪声功率为噪声密度乘上 Df：

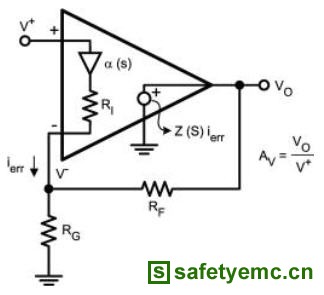
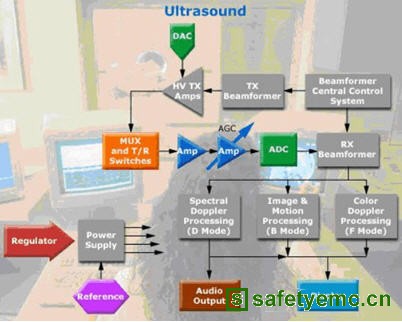
Pth-noise = N0 * Df = s2T，其中 N0 = 噪声频谱密度，单位为 W／Hz。 要在ADC输入端设定数值 N0 需要设计师进行一个端点到端点的讯号路径分析以找出系统噪声指数。参考图 3，各个次系统（接收器、讯号分配放大器、分歧器、与电缆线）具有相对应的增益与噪声指数，整合以上获得如下列公式所示的最后的系统噪声指数（关于更完整的噪声指数的讨论，请参见 [1]）。

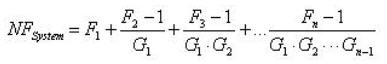 （4）

其中下标表示路径中相连接的次系统（或组件），而参数 Fn 与 Gn 为分析中所包含的各个次系统或组件的线性数值噪声指数与增益。

如果在讯号路径上有数个组件，让设计看起来可能相当复杂。但有一个拯救的方法是 -- 路径中第一个组件会主导最后的系统噪声指数。注意相连接的次系统或组件都列入计算中，其对噪声指数的贡献与其和上传串流次系统增益乘积成反比，也就是说，各下传串流次系统或组件对整体噪声指数具有快速削减的效应。 有经验的系统设计师了解此点，因此路径中第一个组件通常是低噪声放大器，基本上它会将系统噪声指数设定在很低的数值。因此，如果有非常大量来自ADC的讯号路径上传串流，可藉由只观察路径中前面几个次系统（组件）就可获得系统噪声指数良好的合理估计。一旦可估算 NFsys 数值，就可使用公式 5来找出ADC 输入端的噪声功率频谱密度（单位为 dBm/ Hz）：

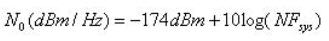（5）

此功率频谱密度相当重要的因素有二。首先，具有宽的输入频宽的ADC可能招致动态范围损失，因为噪声功率（s2T）正比于频宽。其次，虽然基频的处理通常包含滤波器的步骤，以消除未落在所需频带内的噪声，但残留的频带内噪声对整体的SNR的计算也会有贡献。在对数单位中，噪声功率为频谱密度的对数加上所考虑的频宽取 10log的值：

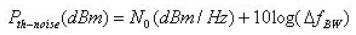（6）

要找出在所需频带中的噪声功率（单位为 dBm），取代讯号频宽为 DfBW：

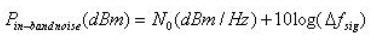（7）

如果单位为 dBm讯号功率已知，可扣除噪声功率以获得单位为 Db的SNR 值，并将之转换为线性数值。或者可以将噪声功率转换为等效的 RMS 电压，并将 SNR 以 RMS 电压来表示：

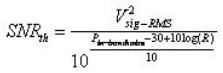（8）

本范例中第二个噪声源为量化噪声。ADC分辨率限制会引入量化噪声（如图6所示）。图中显示一般的平移二元量化器的转换函数。水平轴表示量化器的输入电压范围，分为1 LSB的固定间隔。各个输入电压的取样值对应到这些区间中的一个。

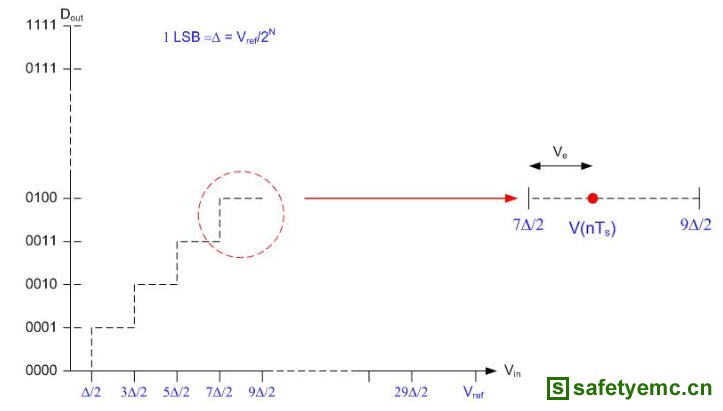
图6 量化器模型

基本上，量化器将取样的电压数值无条件舍去法截取出量化区间中最接近的的整数值。在图6，任何Vin = V（nTs）落在区间 [7D／2,9D／2] 的数值会对应到数位数值 0100。如果将此数字数值转换回电压时，可能会指定一个7D／ 2 =（7／ 2）*（Vref／ 2N）的数值。实际上，真实的电压数值是更大的，因此量化器会引入误差电压，Ve。此误差项（量化噪声）可视为真实讯号数值的外加噪声。因为任何组合的输入电压数值落在特定量化区间的的分布密度是均匀的，因此误差项的分布密度项，或称为量化噪声，也是均匀的。量化噪声功率为此误差项的变异数，即：

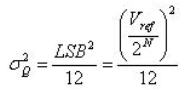（9）

要找出关于此ADC 输入端量化噪声功率，将之除以输入电阻 R。最后，将之除以 Fs／2，可算出量化噪声功率频谱密度：

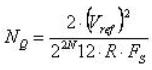（10）

在将此项转换为对数单位dBm之后，如同热噪声一样，可计算出频带内的量化噪声功率，并使用功率值或 RMS 电压值来计算出 SNR。注意此量化噪声功率频谱密度与ADC 分辨率（N）和取样频率（FS）有反比的关系。因此，如果以RMS 电压项来表示SNR，可研究不同的分辨率与取样频率对 SNR的影响。

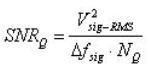（11）

如果取样频率没有抖动，则讯号频带中（频带内）的噪声功率频谱密度会是热噪声与量化噪声的和（在此范例中）。在此情况下，最底线的 SNR 为：

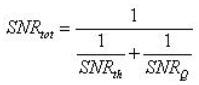（12）

在公式 12中，设计师可以使用这些 SNR项来合成不同的参数的效应，例如取样频率与ADC 分辨率。可以研究这些参数的影响，以定义出以符合目标 SNR（或 ENOB）的边界值。在完成这样的工作尝试选择N 与 FS的数值之后，可以引入由于取样频率抖动所造成的 SNR劣化。在本文的第一部分中显示由于取样频率抖动造成的SNR 为：

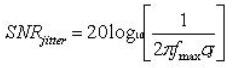（13）

很重要的是要记住在此公式中 sj 实际上是频率RMS 抖动加上ADC 的RMS 孔径抖动的方和根（root-sum-square）值。针对由于抖动造成的SNR使用公式 13，并将之与公式 3 与 12结合，可以建立形成底限SNR的抖动与 SNR 劣化裕度的参数：

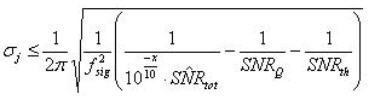（14）

在公式 14中，x 为总 SNR 中由于抖动造成的特定可接受的劣化值（单位为 dB），fsig 为所使用的讯号的最高的频率，以及上述其它的参数。可以根据不等式来设定抖动上限。或者，只要针对特定的应用定义一个目标（最小可接受的）SNR ，并且使用修正的公式 14：

（15）

以WCDMA 系统为例，其讯号中心频率为245 MHz、频宽为5 MHz、操作在61.44 MSPS的取样频率。自动增益控制电路放在ADC 前面，设定用来对讯号功率作平均，在 ADC 输入端产生 -10 dB 全刻度的（dBFS）讯号。ADC 输入范围为 1 Vp-p，且ADC 输入端在 5 MHz 频宽中的热噪声功率设定为 -90 dBm。图7显示三种不同的 ADC 分辨率：8、10、与12 位的图形。在三种情况中，以量化噪声设定噪声背景值。各个情况中，曲线显示当抖动增加时，SNR会劣化。对于12-位 ADC而言，即使当 SNR 从 72 dB 劣化到 59 dB，最大的抖动限制仍可维持在低于 1 皮秒。

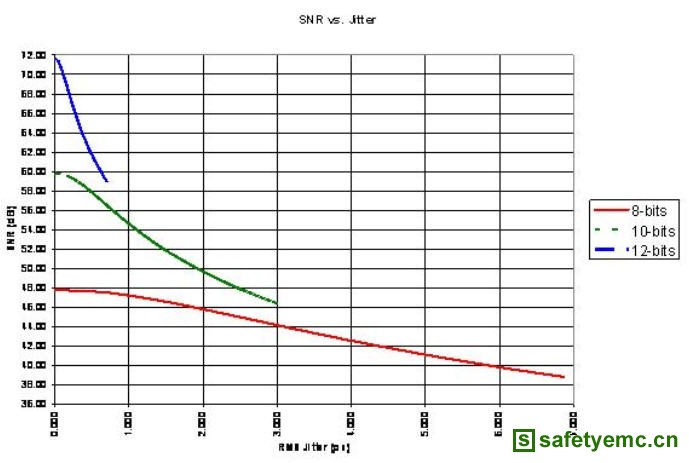
图7 抖动与SNR关系图

结论

本文讨论在使用带通取样来实现高效能多频道、数字接收器架构时，系统设计上所面临的挑战。

对于 ADC而言，要有非常高的输入频宽与高取样频率。本文中强调系统观点的设计，亦即设计选择，例如 ADC 速度与分辨率，以及取样频率需求，可由来自ADC 界面上传串流来定义系统特性。在系统的前端选择适当的低噪声放大器 (LNA)，对整体噪声指数具有重大的影响，也会影响设定ADC 输入端噪声密度。

此外，低噪声取样频率的产生与分配也会主导系统的效能。由于抖动造成的取样噪声对整体 SNR 影响，因此必须搭配所有其它的噪声源造成的影响一起评估，例如热噪声与量化噪声，以决定达成所需的频带内 SNR所需的取样频率效能。

作者简介：Nicholas Gray 任职于美国国家半导体公司数据转换系统部应用工程师，电子邮件:nicholas.gray@nsc.com